Pseudorandom numbers
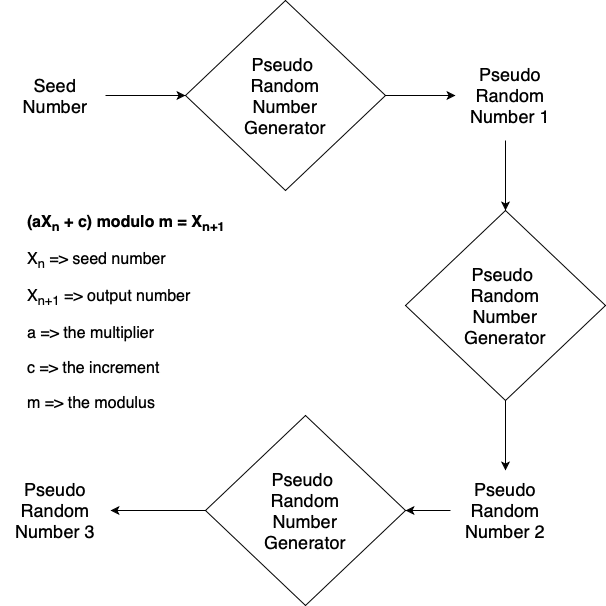
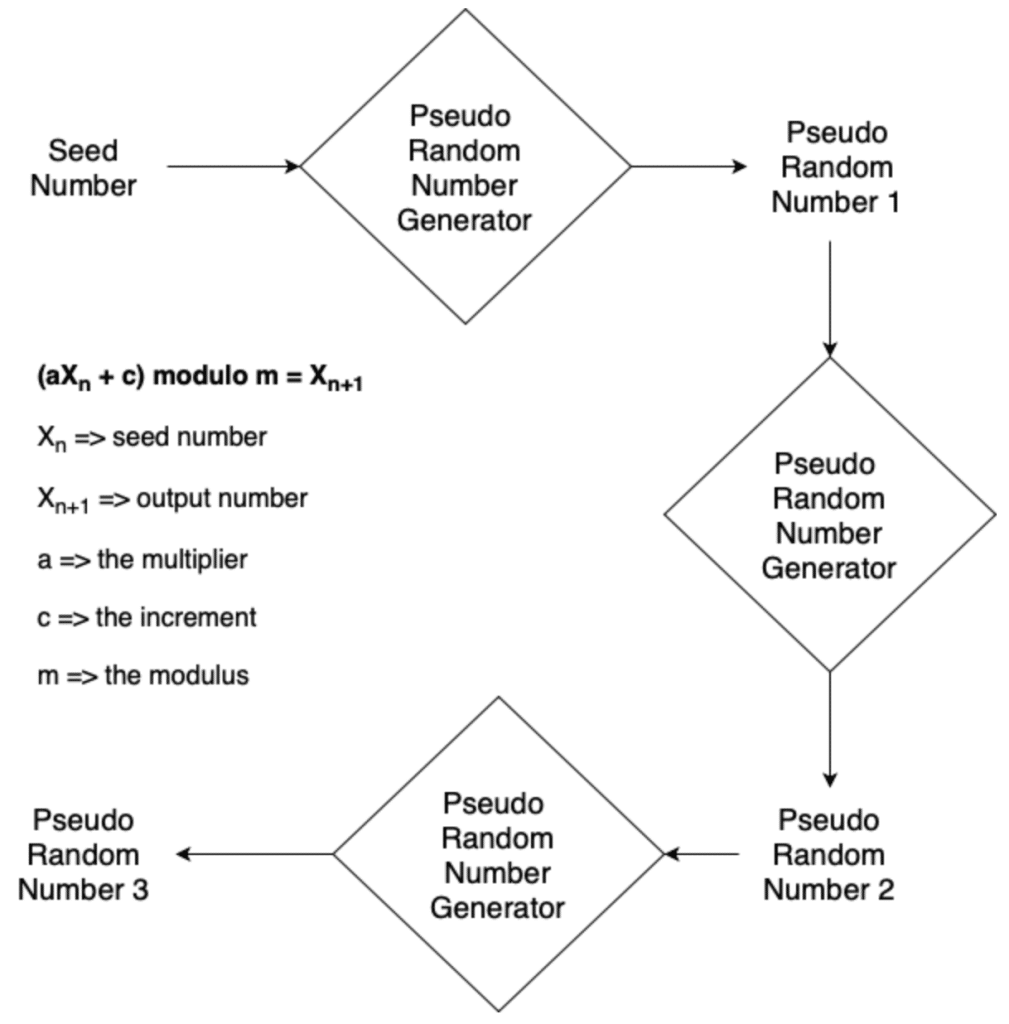
This article will continue our series on cryptography. Our last article discussed random numbers and, in this article, we will learn more about pseudorandom numbers. Pseudorandom numbers are generated by software, using a random “seed” value, and they only appear random. If you knew the initial state, the seed, of the generator function, you would know the complete sequence of all the generated numbers. This is because the generation function produces deterministic, predictable, outputs given a set of inputs. In addition, the generator function will produce outputs that are periodic – the full sequence of random numbers will repeat over and over again.
Another important goal is to generate pseudorandom numbers in such a way that the pattern cannot be determined by statistical analysis. You should only be able to predict the pattern if you know the inputs – not by observing the number sequence.
Pseudorandom numbers are easy to generate at scale and are sufficient for many purposes, even cryptography, as long as the seed is kept private. In fact, for some applications the deterministic nature of PRNGs, versus random number generators, which produce non-deterministic results, are desirable. For example, if you are running simulations, such as Monte Carlo simulations, which require random numbers, as long as you store the seed value for your PRNG, you can replay the simulation at any time.
One example of a PRNG is a linear congruential generator, defined as follows (notice that the m value in the equation below determines the period of your sequence, meaning how many numbers you will have in your pseudorandom number sequence until it repeats):
In programming languages, a very common default PRNG is the Mersenne Twister. This is used by Python, Ruby, PHP as well as by apps such as Excel, Maple and MATLAB.
Next we will discuss cryptographically secure pseudorandom number generators, or CSPRNGs.
